Introduction

In Part 1 of this series on camera calibration, we laid the groundwork by exploring the fundamental principles that govern how cameras translate the 3D world into a 2D image. We delved into camera models and the intrinsic and extrinsic parameters that play a vital role in this transformation. But that was merely scratching the surface.

In this second instalment, I'm going to broaden the scope significantly. We'll venture into the critical importance of camera calibration across various real-world applications—from robotics to autonomous vehicles and even the arts. We'll also uncover the lens distortions that could potentially mar your images and then look at the mathematical equations behind them.

So if you've ever wondered how self-driving cars make sense of their environment, how augmented reality applications manage to superimpose digital elements so naturally, or even questioned the mechanics behind your DSLR's crisp photos, you're in for a treat.

Reasons for Calibration

The importance of camera calibration extends far beyond academic interest—it plays a critical role in various real-world applications. I'll investigate why camera calibration is indispensable in key areas in this section.

1. Robotics and Automation

In robotics, precision is not just a nice-to-have - it is the name of the game. Whether the robots are on bustling factory floors or those designed to help people in their homes- these machines will have to 'know' what is around them and where exactly it is located. This is even more true for robots rocking machine perception tech, which allows them to interpret and make sense of their surrounding. Getting the camera calibration right in settings like these is often a big deal.

Take a factory assembly line, for example. Robots are often kitted out with cameras and machine perception algorithms to identify parts or objects. Mess up the camera calibration, and you're in for a world of trouble. Imagine a robot misjudging the position of a piece it's supposed to pick. That's the kind of error that can start a chain reaction of problems. This is not just about assembly lines or specific tasks, either. Suppose a robot is to pick up an item and place it somewhere specific - a well-calibrated camera ensures that the robot's actions are spot-on with what it is seeing. This is not limited to the task at hand but to the robot's ability to navigate more complex situations. Think about it: a finely calibrated camera can act like a robot's "sixth sense", allowing for on-the-fly adjustments during the job.

To sum it up, nailing camera calibration in robotics and automation isn't just a good practice; it is a must. Whether for aiding complex tasks or helping a robot safely navigate an unstructured environment, getting the camera settings right can either make or break the whole operation.

2. Autonomous Vehicles

We are on the brink of a game-changer - self-driving cars are about to become a common sight on our roads. But let us not forget, the tech making this possible is anything but simple. At the core, we have advanced vision systems that let these vehicles 'see the world around them. However, is not always enough; these systems must also be spot-on when interpreting this visual data for real-time decision-making. This is precisely where camera calibration comes in and becomes a critical piece of the puzzle.

For a minute, think about the challenges of driving autonomously. Cars must navigate a world filled with other vehicles, pedestrians, and other unpredictable elements. Oh, get the camera calibration wrong, and you are asking for trouble. Results of miscalibration? We are discussing potentially misjudging the distance to the car in front, which could translate to insufficient time to brake or even a full-on collision.

Here is the kicker: autonomous cars rely on many machine vision tasks - such as detecting obstacles, understanding road signs, or even interpreting road markings. Many of these cars would require more than one camera, each serving a specific purpose. Hence, calibrating each camera is not a one-off job- it is about ensuring all these cameras work harmoniously.

3. Augmented and Virtual Reality

Okay, let's talk AR and VR. These are realms where the line between the digital and the real world gets blurry. Whether overlaying virtual furniture in your real living room or immersing yourself in a completely digital world, the experience has to feel real. That's why camera calibration is a big deal in AR and VR tech.

Think about it. You put on a VR headset and step into a virtual world. You move your head, and the perspective changes perfectly in sync. That's not magic—it's precise calibration. If the camera's off even by a little, you might start to feel motion sickness or have a subpar experience. That's the last thing you want when battling space pirates or exploring a virtual museum.

Now, switch gears to AR. Imagine using an app on your smartphone to visualize how a new sofa would look in your living room. The app has to blend digital objects with the real world smoothly. If the camera calibration is off, that sofa might look like it's floating in mid-air or sinking into the floor. Not the best way to make a buying decision, right?

And let's not forget about more advanced applications. For example, getting the camera calibration wrong could be life and death in medical AR. Surgeons often use AR tech for guided procedures. In scenarios like this, the calibration needs to be absolutely spot-on for accurate guidance and successful outcomes.

So, all in all, whether you're gaming, shopping, or even performing surgery, camera calibration in AR and VR isn't just about enhancing the experience—it's about making it possible in the first place.

4. Film and Photography

Let's get into film and photography, where camera calibration isn't just about the tech—it's also about the art. In settings that demand a heavy dose of scientific rigor, like wildlife documentaries or high-speed sports action, getting your camera settings right is non-negotiable. Picture this: you're shooting a documentary on migratory birds. A well-calibrated camera lets you capture beautiful shots and accurate data on how fast and high these birds fly. That's adding a layer of scientific credibility to your storytelling.

But hey, it's not all about the numbers. Camera calibration also plays a starring role in the artistic side of things. Take landscape photography, for instance. You want those mountain ranges and valleys to look as majestic in the photo as they do in real life. A calibrated camera ensures that the proportions and spatial relationships within the frame are just right, enhancing your shots' emotional impact and narrative quality.

And let's not forget the controlled chaos of a studio setting. Calibration is your best friend, whether you're doing product photography, snapping high-fashion looks, or capturing fine art reproductions. In essence, camera calibration in film and photography is more than a behind-the-scenes technicality; it's a linchpin that can elevate your work from good to great. It's not just about getting the colour balance or the focus right; it's about capturing the subject's soul, be it a fast-paced sporting event or a still life. When your camera is finely tuned, your work speaks volumes—conveying scientific facts or evoking deep emotions.

Types of Distortion

Regarding camera calibration, addressing distortions is not just a side quest - it is the main objective. Distortions are discrepancies between the captured image and the real-world scene, affecting the accuracy of the camera's representations. Distortions can be characterised as deviations from the ideal imaging model, where rays from a single point in three-dimensional space converge at a single point on the imaging sensor. Numerous factors contribute to distortions, including lens shape, refractive index variations, and manufacturing imperfections. These distortions have various types, each with a mathematical model and correction method. Understanding these distortions is pivotal for calibrating the camera to achieve high accuracy in multiple applications.

A. Radial Distortions

1. Barrel Distortions: Barrel distortion is a sub-type of radial distortion, where straight lines appear to curve outward from the centre of the image.

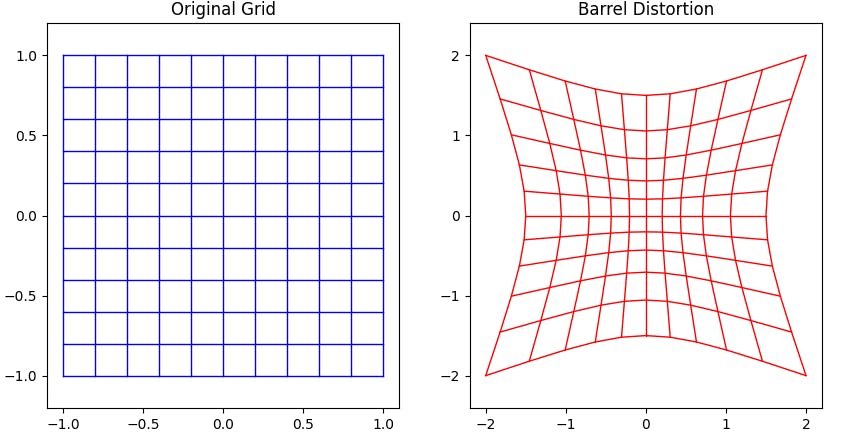
The image magnification decreases with distance from the optical axis. This causes straight lines near the edge of the field to bend inward, resembling the shape of a barrel. This type of distortion is common in wide-angle lenses.

2. Pincushion Distortion: Conversely, image magnification increases with the distance from the optical axis in pincushion distortion. The result is that straight lines bend outward from the centre, akin to a pincushion

Mathematically, a unified model can represent both barrel and pincushion distortions, often employing higher-order polynomials, which is particularly useful when working with more complicated lens systems. The general formula is:

$$\begin{align*} x' &= x\left(1 + k_1 r^2 + k_2 r^4 + \ldots\right) \\ y' &= y\left(1 + k_1 r^2 + k_2 r^4 + \ldots\right) \end{align*}$$

Here, (x, y) are the original coordinates, (x', y') are the distorted coordinates, k₁, k₂, ... are the distortion coefficients, and r is the radial distance from the centre of the image, calculated as:

$$r = \sqrt{x^2 + y^2}$$

In this general model:

• A positive k₁ will produce pincushion distortion, as lines will curve outward.

• A negative ***k₁***​ will produce barrel distortion, where lines curve inward towards the centre.

• Higher-order terms like ***k₂***​ allow for more complex distortion patterns, which might be observed in higher-end or more flawed lens systems.

The model is extendable to as many terms as necessary, but in practice, most systems are sufficiently modelled using just k₁ and sometimes k₂.

B. Tangential Distortions

These distortions occur when the lens and the imaging plane are not parallel. Tangential distortions usually shift the image in a direction orthogonal to the radial distortions and can make the image look tilted or skewed. While radial distortions affect the image in a radially outward direction from the centre, tangential distortions act orthogonally to them. This means that they can make the image appear tilted or skewed, effectively moving the distorted image points horizontally and vertically in a way unrelated to their distance from the optical axis.

Mathematically, tangential distortion can be expressed as:

$$\begin{align*} x' &= x + \left(2p_1 xy + p_2 (r^2 + 2x^2)\right) \\ y' &= y + \left(p_1 (r^2 + 2y^2) + 2p_2 xy\right) \end{align*}$$

Here, x' and y' are the distorted coordinates. x and y are the original coordinates, and r is the radial distance from the origin, calculated as r = √(x² + y²).

The coefficients p₁ and p₂ are the tangential distortion coefficients. These terms aim to correct the tilt in the lens and bring the captured image closer to what would be charged if the lens were perfectly aligned. By adjusting the coefficients during the camera calibration process, one can minimize the effects of tangential distortions.

Conclusion

In this second instalment, we've delved deeper into the reasons for camera calibration across various industries, touched on different types of distortions, and hinted at the mathematics involved. However, we've only scratched the surface. In Part 3, we'll dive into the heart of the mathematics that makes accurate camera calibration possible. From optimization problems to factoring in distortions, we'll explore how all these elements combine to create a robust camera model. Stay tuned!

References

For those looking to delve deeper into the topics covered in this blog post, the following resources are highly recommended:

[1] Codes for distortion plots

[2] Multiple View Geometry in Computer Vision by Richard Hartley and Andrew Zisserman

[2] Stanford CS231A: Camera Models